Introduction to FLOOR.MATH
The FLOOR.MATH function in Excel rounds a number down to the nearest integer or to the nearest multiple of significance. It’s part of Excel’s mathematical functions and provides more control over rounding behavior than the older FLOOR function.
Arguments Explained
| Argument | Required/Optional | Description |
|---|---|---|
| number | Required | The number you want to round down. |
| significance | Optional | The multiple to which you want to round. Default is 1. |
| mode | Optional | Controls rounding direction for negative numbers. Use 0 for away from zero, or 1 for toward zero. Default is 0. |
Note: FLOOR.MATH is available in Excel 2013 and later versions. For earlier versions, use the FLOOR function, but be aware of differences in how negative numbers are handled.
Practical Examples of FLOOR.MATH
Rounding down 24.7 to the nearest integer:
=FLOOR.MATH(24.7)
The significance and mode arguments are optional. If only the number argument is used the FLOOR.MATH function will make the number go down (to the floor) to the next integer.
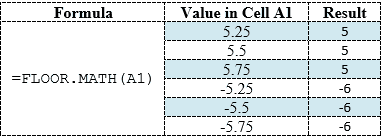
Rounding down 24.7 to the nearest multiple of 5:
=FLOOR.MATH(24.7, 5)
Rounding down -24.7 to the nearest integer:
=FLOOR.MATH(-24.7)
Rounding down -24.7 to the nearest integer with mode=1 (toward zero):
=FLOOR.MATH(-24.7, 1, 1)
Using the Mode argument
Any nonzero value used for the mode argument will reverse the normal direction for the FLOOR.MATH function by making a negative number round up.
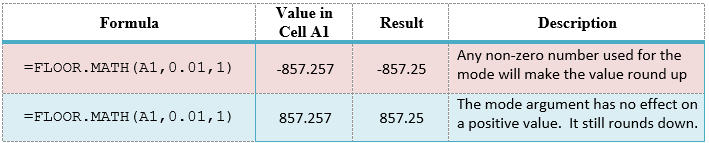
Rounding down $24.37 to the nearest nickel (0.05):
=FLOOR.MATH(24.37, 0.05)
Lowered to the nearest penny:

Lowered to the nearest nickel:

Lowered to the nearest quarter:
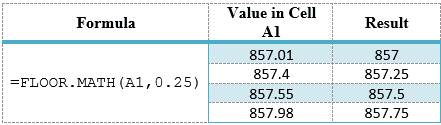
Lowered to the nearest hundred dollars:

Lowered to the nearest thousand dollars:

Tip: When working with inventory or quantities, use FLOOR.MATH to ensure you don’t overestimate available resources.
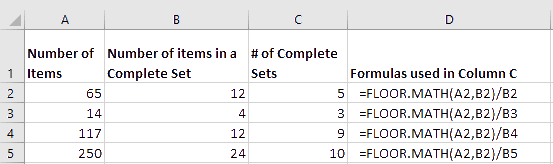
Use FLOOR.MATH to determine the number of complete sets.
The FLOOR.MATH function can also be used to determine how many complete sets there are in a given number. For example, how many full dozens are there in 28, how many full grosses are there in 300, how many full days are there in 125 hours, etc. Looking at row 2 in the table below we have 65 items. We want to know how many full sets of 12 are in 65. We will first use the FLOOR.MATH function to round down to the nearest multiple of 12. We will use the formula =FLOOR.MATH(A2,B2) to round down the value 65 to the next multiple of 12 which gives us a result of 60. Now we can take that value and divide it by the number of items in a complete set which is 12. This gives us a result of 5 which is the number of complete sets in 65. The formulas entered in column C are displayed in column D.
Try It Yourself
Experiment with the FLOOR.MATH function using different values:
Common Use Cases
1. Inventory Management
When calculating how many complete units can be made from available materials, FLOOR.MATH ensures you don’t overestimate production capacity.
2. Financial Calculations
When working with financial data, you might need to round prices down to comply with certain pricing policies or to stay within budget constraints.
3. Data Analysis
When creating histogram bins or grouping data, FLOOR.MATH helps establish lower bounds for each category.
4. Time Calculations
When calculating complete time periods that have passed (like completed hours or days), FLOOR.MATH gives you the appropriate value.
Comparison with Other Rounding Functions
| Function | Purpose | Example |
|---|---|---|
| FLOOR.MATH | Rounds down to nearest multiple with control for negative numbers | =FLOOR.MATH(4.8, 1) → 4 |
| CEILING.MATH | Rounds up to nearest multiple with control for negative numbers | =CEILING.MATH(4.2, 1) → 5 |
| ROUND | Rounds to specified number of digits | =ROUND(4.25, 1) → 4.3 |
| ROUNDUP | Always rounds up to specified number of digits | =ROUNDUP(4.2, 0) → 5 |
| ROUNDDOWN | Always rounds down to specified number of digits | =ROUNDDOWN(4.8, 0) → 4 |
Fun Facts about Rounding and FLOOR.MATH
Floor in Mathematics
The floor function in mathematics, written as ⌊x⌋, gives the greatest integer less than or equal to x. This is exactly what FLOOR.MATH does when the significance is 1!
Excel Evolution
FLOOR.MATH was introduced in Excel 2013 to provide better compatibility with international standards and improve the handling of negative numbers compared to the original FLOOR function.
The Opposite of Ceiling
Just as a ceiling is above you, the mathematical floor is below you – hence the name for this function that always rounds downward!
Computer Science Connection
Floor and ceiling functions are fundamental in computer science algorithms, particularly in areas like memory allocation, array indexing, and efficiency calculations.
Language Consistency
Excel introduced the .MATH suffix to both FLOOR and CEILING functions to create a consistent pair of functions that behave predictably across all types of numbers.